Big O Notation

 

🙄빅오 표기법이란 ?

• 빅오 표기법은 알고리즘의 효율성을 표기해주는 표기법이다.
• 코드를 분류하거나 비교할 수 있는 시스템
• 대략적으로 숫자를 세는 것의 붙인 공식적인 표현
• 입력된 내용이 늘어날 수록 알고리즘에 실행시간이 어떻게 변하는 지 설명하는 공식적인 방식
• 입력된 N의 따라 걸리는 시간의 전반적인 추세

ex) 예를 들어 "문자열을 받아 뒤집어서 출력하는 코드를 작성하시오" 라는 문제가 있다고 해보자
그렇다면 어떻게 작성하는 것이 가장 효율적인 방법일까?

이 문제에 대해 접근 방식과 해결 로직을 작성하는 데 고민할 때 적용할 수 있는 것이 Big O Notation이다.

Add1

function addUpto(n) {
    let total=0
    for(let i=1;i<=n;i++){
        total+=i
    }
    return total
}

let t1= performance.now()
addUpto(1000000000)
let t2=performance.now()
console.log(`Time1 Elapsed: ${(t2-t1)/1000} seconds`)
console.log(addUpto(3)) // 6 

Add2

function addUpTo(n) {
    return n*(n+1)/2
}
let t1= performance.now()
addUpto(1000000000)
let t2=performance.now()
console.log(`Time1 Elapsed: ${(t2-t1)/1000} seconds`)
console.log(addUpTo(3)) // 6 

위 두 함수는 1부터 입력받은 숫자까지 모두 더해주는 함수이다. 기능은 똑같지만 코드는 조금 차이가 있다.
여기서 위 2가지 방법 중 어느 코드가 더 좋은 코드일까? 그리고 더 좋은 코드가 되는 기준은 무엇일까?

🤩 더 나은 코드를 가지는 기준..?

• 속도?
• 메모리 사용량
• 가독성?
• => 속도를 보기 위해 위와 같이 코드를 추가하고 살펴보자
  Add1의 경우 1.2416초 정도 나오고
  Add2의 경우 0.00100초가 나와 두번째가 속도면에서 더 좋다고 할 수 있다.
  하지만 속도만으로 코드가 성능이 좋다고 평가하기엔 이르다.

😑 속도가 가지는 문제

• 기계에 따라 속도 측정은 다르게 나올 수 있다.
• 똑같은 기계가 다르게 시간을 측정할 수도 있다.
• 알고리즘은 정말 빠르게 처리한다.👀그렇다면 무엇을 가지고 평가하는 것이 좋을까?

정확하게 평가하기가 어렵다.
컴퓨터가 처리해야하는 연산 개수를 세면 된다. => 어떤 컴퓨터든 연산을 처리해야하는 개수는 똑같다.
컴퓨터마다 성능 차이는 있지만 코드에 따라 연산처리 개수는 달라지고 시간은 연산의 횟수에 달려있다.

😏문제해결?!?

Add2의 경우 연산은 3번 한다.

위에서 작성한 함수 2개를 다시 한 번 살펴보면 *, +, / 이렇게 3번 한다.

Add1을 봐보쟈

function addUpto(n) {
    let total=0
    for(let i=1;i<=n;i++){
        total+=i
    }
    return total
}

+=로 한 번만 있는 것 같지만 반복문 안에 있다. 즉 들어온 숫자만큼 연산을 수행한다.
즉 n개수의 연산이다. 그 외에도 for문 안에 있는 =, ++ 등 모든 연산이 n의 따라 증가한다.

😎 Big O Definition

• 선형 (f(n)=n)
• 제곱 (f(n)=n2)
• 상수 (f(n)=n)
• 다른 무언가

=> 실행시간이 갖을 수 있는 최대치

ex) Add2를 보면 연산이 3개로 고정되어 있어 상수 (f(n)=n)으로 볼 수 있다. 즉 일자로 된 상수함수를 갖는다.
=> 이럴경우 O(1)라고 표기한다.

 Add1의 경우 N과 연산의 개수가 상관이 있다. 따라서 O(n)이라고 표기한다.
   이중 for문의 경우에는 O(n2(제곱))이 것이고 연산의 개수에 따라 걸리는 시간은 제곱으로 늘어난다.
이렇게 연산 N의 따라 전반적으로 소요되는 시간을 표기하는 것을 빅 오 표기법이라고 한다. 

😉 Big O 단순화 하기

 결국 Big O를 보면서 알 수 있는 것은 무한대처럼 대략적으로 정확한 큰 그림을 말한다. 
따라서 상수는 딱히 중요하지 않다.

상수 
O(2N) -> O(N)  => 항상 납작한 그래프  
0(500) 

제곱 
O(13N2) => O(N2)

하지만 이렇게 단순화 된 것만 보고도 어떤 것이 가장 빠르고 느린지를 알 수 있다. 

작은 상수도 전혀 상관없다 
O(N+10) => O(N) 

O(N2 + 5N+8) ==> 0(N2) 

위와 같이 무한대처럼 O 표기법은 크게 보면서 단순화 하는 것이 중요하다.

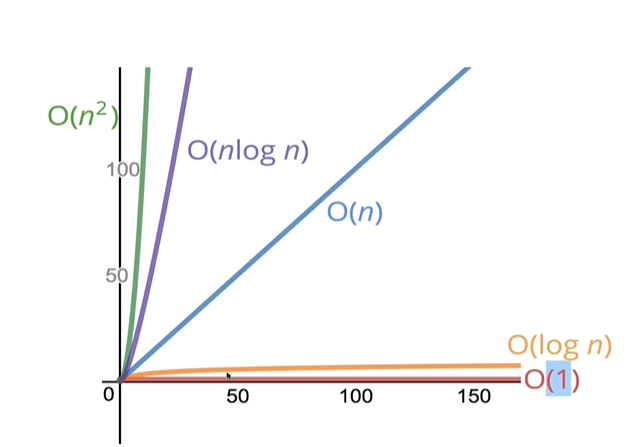
🤗 Big O 표기 그래프