계수 정렬의 시간 복잡도는 O(N)으로 굉장히 빠르다.
기존 정렬들과 다른 점은 각 인덱스에 위치한 값들을 서로 바꾸어주는 것이 아니라 값의 크기를 기준으로 개수를 세는 알고리즘이다. 단! 범위 조건이 있는 조건에 한해서만 빠른 알고리즘이다.
예시를 보면 1 ~5까지 범위의 제한이 있다.
1 2 1 3 5 3 4 2 1 5 2 4 3 1 2 3 2 5 5 2 3 2 1 5 5 4 2 3 1 1
만약 이렇게 되어있다면
1. 0인덱스 1 2 1 3 5 3 4 2 1 5 2 4 3 1 2 3 2 5 5 2 3 2 1 5 5 4 2 3 1 1
| 크기 | 1 | 2 | 3 | 4 | 5 |
| 개수 | 1 | 0 | 0 | 0 | 0 |
2. 1 인덱스 1 2 1 3 5 3 4 2 1 5 2 4 3 1 2 3 2 5 5 2 3 2 1 5 5 4 2 3 1 1
| 크기 | 1 | 2 | 3 | 4 | 5 |
| 개수 | 1 | 1 | 0 | 0 | 0 |
3. 2 인덱스 1 2 1 3 5 3 4 2 1 5 2 4 3 1 2 3 2 5 5 2 3 2 1 5 5 4 2 3 1 1
| 크기 | 1 | 2 | 3 | 4 | 5 |
| 개수 | 2 | 1 | 0 | 0 | 0 |
4. 3 인덱스 1 2 1 3 5 3 4 2 1 5 2 4 3 1 2 3 2 5 5 2 3 2 1 5 5 4 2 3 1 1
| 크기 | 1 | 2 | 3 | 4 | 5 |
| 개수 | 2 | 1 | 1 | 0 | 0 |
5. 4 인덱스 1 2 1 3 5 3 4 2 1 5 2 4 3 1 2 3 2 5 5 2 3 2 1 5 5 4 2 3 1 1
| 크기 | 1 | 2 | 3 | 4 | 5 |
| 개수 | 2 | 1 | 1 | 0 | 1 |
...
이렇게 크기를 기준으로 COUNT해주기 때문에 빠르게 정렬을 할 수 있다.
1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 3 3 3 3 3 3 4 4 4 5 5 5 5 5 5
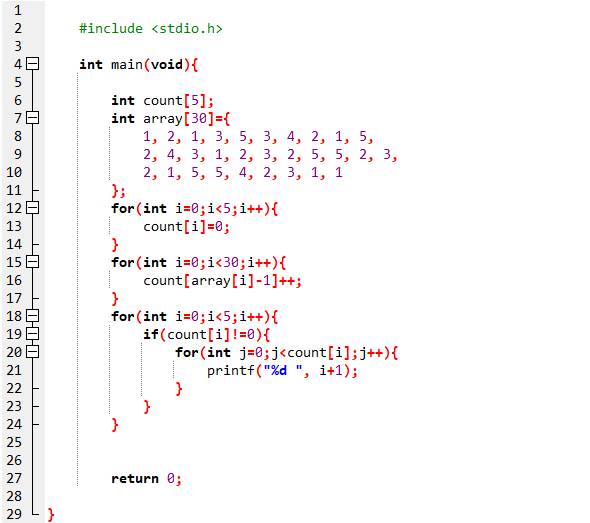
12번 라인은 각 count배열의 값을 0으로 초기화 시켜주고
15번 라인은 값의 크기에 맞는 array값의 개수를 넣어주는 것이다.
18번 라인은 이제 각 count의 값의 크기에 맞는 개수를 출력해준다.

이렇게 모든 데이터 크기가 1부터 5사이 이기 때문에 O(N)인 속도로 정렬을 수행할 수 있다.
'알고리즘' 카테고리의 다른 글
| C++STL sort()함수 (0) | 2021.11.02 |
|---|---|
| 병합 정렬(Merge Sort) (0) | 2021.11.01 |
| 퀵 정렬 (0) | 2021.10.30 |
| 삽입정렬 (0) | 2021.10.30 |
| 버블정렬 (0) | 2021.10.30 |




댓글